Ni seulement le couple surface et densité.
C’est, surtout, la structure — plus ou moins fractale — de l’espace (laquelle est déterminée par la façon dont celui-ci est engendré
La ville n’est jamais produite d’un seul geste
)
Dans les endroits denses, chacun se contente de quelques mètres carrés. Que l’on paye cher, très cher.
Pourquoi ?
Parce qu’au-delà d’une surface habitable, nous recherchons une expérience. Et que celle-ci n’est proportionnelle
ni à la taille, ni à la densité de l’espace urbain, mais au nombre et à la qualité des options disponibles
L’optionalité, cette propriété qui nous permet de faire de l’imprévu un atout
.
1. Parlons taille, surface, densité et fractalité
Et des dimensions cachées — mais bien perçues et valorisées — de l’espace urbain.
Nous avons tous appris à l’école qu’une ligne est un objet géométrique à une dimension : on la mesure par sa longueur, qu’on peut étalonner par le mètre
(ou le pied
).
Nous savons, ensuite, que les surfaces ont deux dimensions et qu’elles sont mesurées par des petits bout de surface que l’on appelle des mètres carrés
.
Les objets enfin, ont trois dimensions : longueur, largeur, hauteur (sous plafond, par exemple).
Dans cet espace physique à trois dimensions, nous le sentons bien, l’espace est limité.
Ce que nous savons moins, c’est qu’il existe des hyper espaces.
2. Les hyper lignes
Entre les lignes et les surfaces existent des objets, comme les flocons de neige, qui sont des lignes qui se rapprochent des surfaces
par leur structure fractale
L’expérience enveloppante de la fractalité du bâti
.
Le flocon de Koch
La géométrie — fractale — des villes dans lesquelles les décisions sont distribuées
a une dimension de 1,26 (dimension fractale D = log(4)/log(3) ≈ 1,2619) : il se manifeste dans un espace, un monde que nous ne soupçonnions pas, qui se situe entre le monde des lignes et celui des surfaces
.
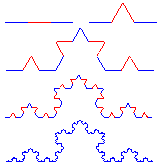
flocon de Kochest une courbe construite récursivement à partir d’un segment initial. À chaque itération, chaque segment est remplacé par quatre segments de longueur 1/3 du segment précédent. Le nombre de segments Nₙ après n itérations est Nₙ = 4ⁿ, et leur longueur individuelle est εₙ = (1/3)ⁿ. La dimension fractale D est définie par :
D = limₙ→∞ [log(Nₙ) / log(1/ εₙ)]= log(4) / log(3) ≈ 1,2619
Cette courbe possède une longueur infinie, mais est contenue dans un espace fini. Elle illustre parfaitement la notion d’objet de dimension non entière, situé entre la ligne (1) et la surface (2). C’est un modèle canonique pour penser les structures auto-similaires, récursives, et topologiquement complexes.
Sur une surface, qui est un espace à deux dimensions (la glace d’une patinoire), nous avons une infinité d’itinéraires possibles pour aller d’un point A à un point B.
A l’inverse, en TGV, un seul itinéraire possible entre Bordeaux et Paris : une seule ligne, dans un espace à une dimension.
En ville, le réseau des voies nous propose une expérience qui oscille entre ces deux extrêmes, selon les lieux : dans un centre-ville médiéval (ou dans le métro parisien) on a toujours un grand choix d’options pour aller d’un point A à un point B. La dimension du réseau se rapproche de 2.
Dans les lotissements périurbains (ou sur le réseau du RER de banlieue), le nombre d’itinéraires s’effondre… et la dimension du réseau se rapproche de 1.
3. Les hyper surfaces
Entre les surfaces et les volumes existent, là encore, des espaces, des mondes à découvrir : ceux qu’explorent, par exemple, les dentelles des sculpteurs qui produisent ces façades ornées
Emboitements et ornements : la fractalité du bâti, jusqu’à l’infiniment petit
, divisées
La transformation des lotissements par la division parcellaire
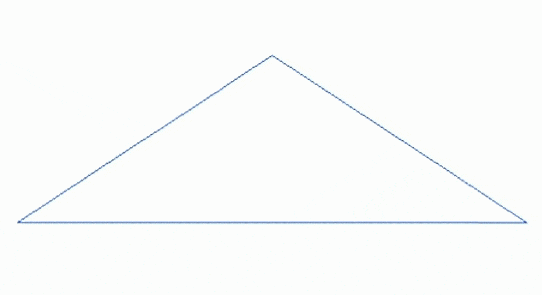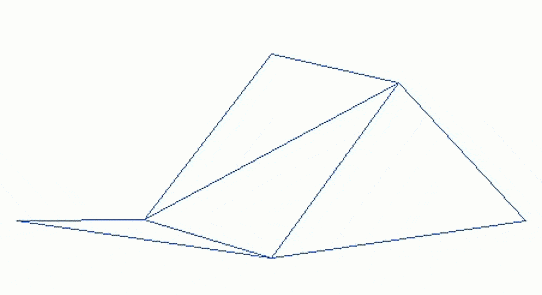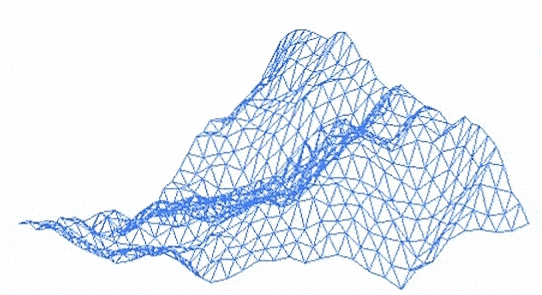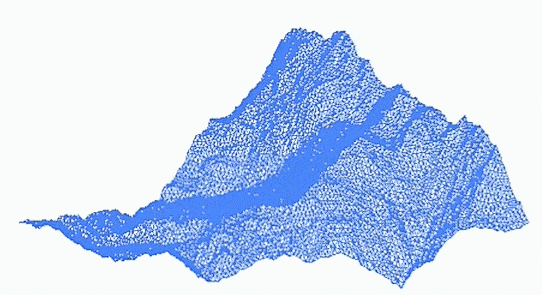, raffinées de façon récursive
Pourquoi certaines villes donnent le sentiment d’avoir été « engendrées » plutôt que dessinées ?
, jusqu’à présenter des formes fractales.
Ces façades, qui sont plus que des surfaces
, offrent à l’expérience (du regard, cette fois) un nombre indéfini d’options, d’itinéraires.
