Que se passe-t-il quand on double le nombre d’habitants d’une ville ?

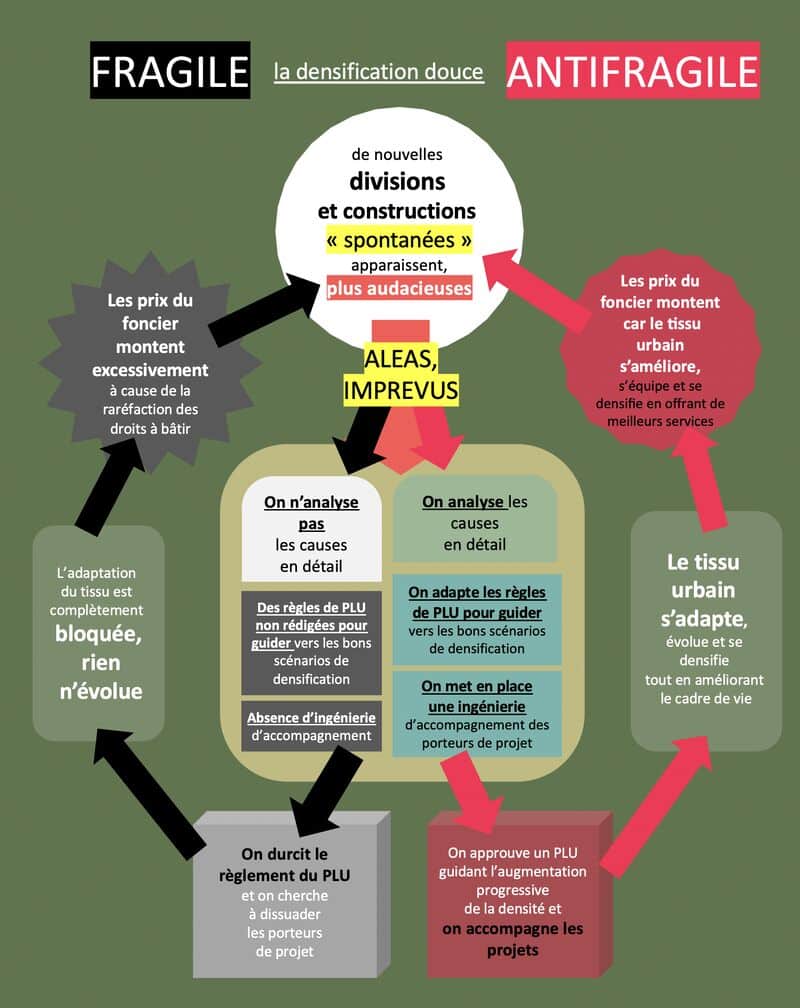
J’ai développé une idée simple mais qui me semble décisive : tous les phénomènes urbains ne relèvent pas des mêmes régimes statistiques Certains phénomènes sont gouvernés par la moyenne. D’autres par les extrêmes. .

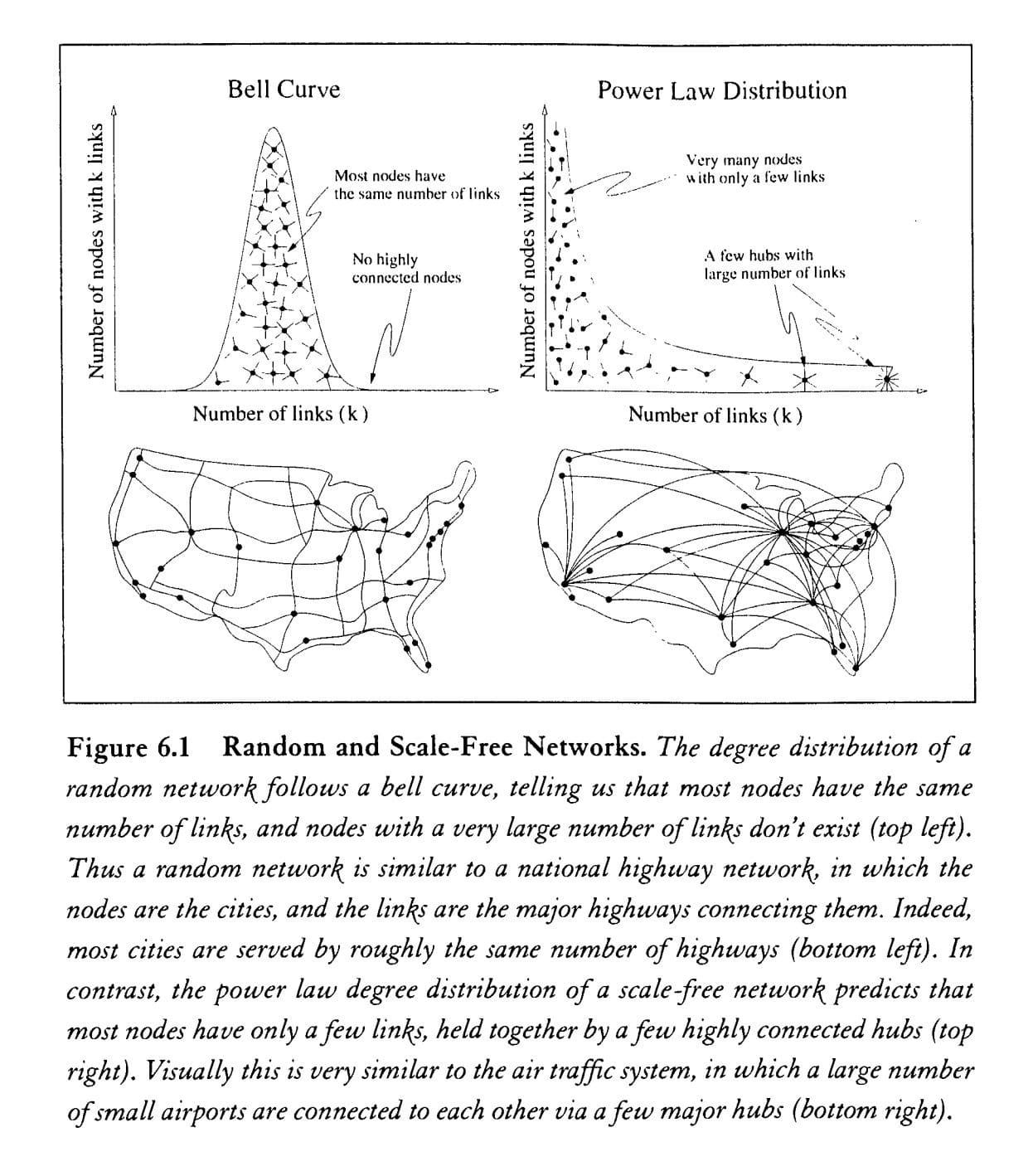
• Certains obéissent à une loi normale : leur distribution est centrée sur une moyenne, les écarts sont modérés, les cas extrêmes rares.
• D’autres relèvent d’une loi de puissance ¹²: leur distribution est dominée par l’impact des extrêmes.

Or ce sont ces phénomènes asymétriques qui jouent un rôle structurant, souvent sans qu’on s’en aperçoive.

Et c’est Nassim Taleb qui a donné à cette distinction une portée stratégique, en nommant ces deux  mondes  « Extrêmistan » VS « Médiocristan » : deux régimes statistiques à bien distinguer pour mieux penser — et surtout faire la ville qui s’entremêlent dans la réalité, et qui brouillent les pistes de l’urbaniste :

• le  Médiocristan , monde des moyennes, où l’on peut prévoir, planifier, contrôler,
• et l’ Extrêmistan , monde des extrêmes, où l’on doit développer des stratégies d’adaptation, de robustesse et d’antifragilité.

Pour approfondir cette distinction statistique dans le fonctionnement concret des villes, un détour par les lois d’échelle¹² de Geoffrey West s’impose. Elles ne mesurent pas la fréquence des événements, mais la façon dont les phénomènes urbains évoluent avec la taille des villes — et révèlent, par contraste, ceux qui s’amplifient, se diluent ou s’accumulent. Physicien, ancien président du Santa Fe Institute, West a étudié les données de plus de 350 villes américaines.

Sa question : que se passe-t-il quand une ville double de population ?

Réponse : tout ne double pas.

Les phénomènes urbains se répartissent en trois catégories :

1. Les phénomènes linéaires (exposant ≈ 1)

• Liés aux besoins biologiques ou logistiques : repas, eau, déchets…
• Ils augmentent proportionnellement à la population.
• 2× plus d’habitants → 2× plus de bouches à nourrir.

2. Les phénomènes sous linéaires (exposant ≈ 0,85)

• Infrastructures physiques et ressources mutualisables : voirie, réseaux, surfaces bâties, énergie, consommation de ressources matérielles…
• Ils augmentent moins vite que la population (économie d’échelle)
•  You don’t need twice the number of roads, only about 85% more. 

3. Les phénomènes super linéaires (exposant ≈ 1,15)

• Dynamiques sociales : revenus, brevets, interactions, criminalité, innovation, restaurants, événements culturels, spectacles…
• Ils augmentent plus vite que la population.
•  You get 115% more income, patents, and crime. 

Passage à l’échelle : par rapport à une ville de 10’000 habitants, une ville de 1 million d’habitants (100× plus grande) aura en moyenne :

• 100× plus de déchets ménagers à collecter,
• 40× plus de routes à entretenir,
• 140× plus de restaurants.

Pour résumer :

• Ce qui relève des besoins physiques individuels → linéaire (logique additive) ;
• Ce qui relève des infrastructures partagées → sous-linéaire (économies d’échelle) ;
• Ce qui relève des interactions humaines → super-linéaire (logique multiplicative).

Notes :